0%

(CVPR 2018) Boosting Adversarial Attacks with Momentum

Posted on In ,

Keyword [MI-FGSM] [Ensemble]

Dong Y, Liao F, Pang T, et al. Boosting adversarial attacks with momentum[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2018: 9185-9193.


1. Overview

1.1. Motivation

  • most of existing adversarial attacks can only fool a black-box model with low success rate

In this paper, it proposed a broad class of momentum-based iterative algorithm

  • stabilize update diretions
  • escape from poor local maximum
  • more transferable adversarial examples
  • alleviate the trade-off between the white-box attacks and the transferability
  • apply momentum iterative algorithms to an ensemble of models (further improve the success rate for black-box attacks)

1.2. Generally

  • Transferability. different machine learning models learn similar decision boundaries around a data point.
  • one-step gradient-based methods more transferable

1.3. Contribution

  • momentum iterative gradient-based methods
  • study several ensemble approaches
  • first to show models obtained by ensemble adversarial training with a powerful defense ability are also vulnerable to the black-box attacks

1.4.1. Attack Methods

  • one-step
  • iterative
  • optimization-based methods. lack the efficacy in black-box attacks just like iterative methods


1.4.2. Defense Methods

  • inject adversarial examples into training procedure
  • ensemble adversarial training


2. Methods

the assumption of linearity of the decision boundary around the data point may not hold when the distortion is large.

  • FGSM. underfit
  • iterative FGSM. overfit

2.1. MI-FGSM



  • g_t. gather the gradient of the first t iterations with a decay factor μ
  • μ=0. MI-FGSM→ iterative FGSM
  • gradient normalized by L1 distance, the scale of the gradients in different iterations varies in magnitude

2.2. MI-FGSM for Ensemble Model

  • ensemble in logits (input values to softmax). perform better


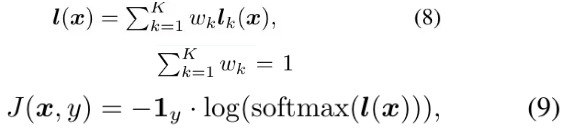
  • ensemble in prediction probability


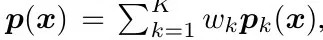
  • ensemble in loss



2.3. Extension

  • L2 distance


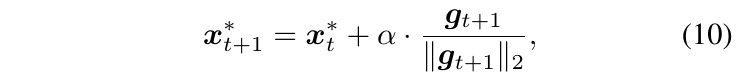
  • targeted attacks


3. Experiments

3.1. Single Model



  • maximum perturbation = 16
  • μ = 1

3.1.1. Decay Factor μ



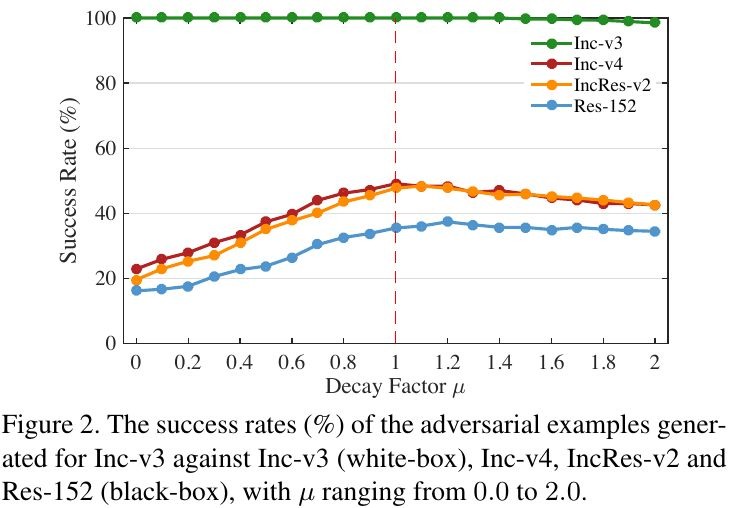
  • μ=1. adds up all previous gradients to perform the current update

3.1.2. The Number of Iteration



  • when increasing the number of iterations, the success rate of I-FGSM against a black-box model gradually decreases

3.1.3. Update Direction

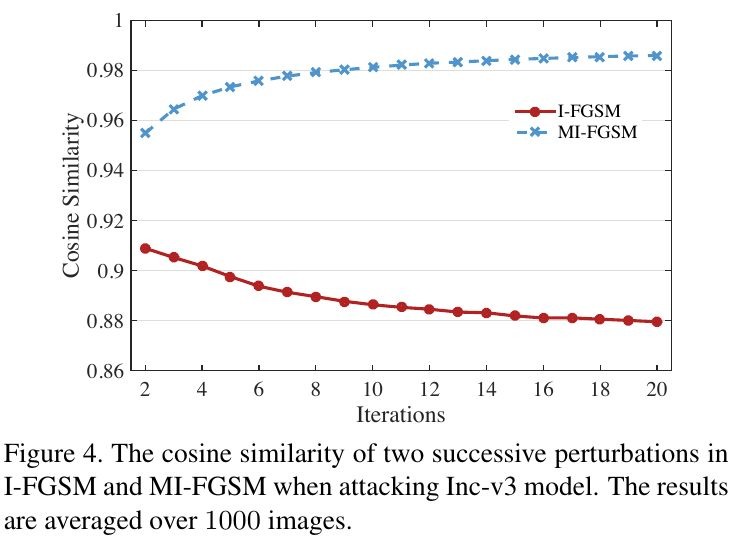
  • update direction of MI-FGSM is more stable than I-FGSM (larger cosine similarity)
  • stabilized updated directions make L2 norm of the perturbation lager, which helpful for transferability


3.1.4. The Size of Perturbation

  • α = 1


3.2. Ensemble



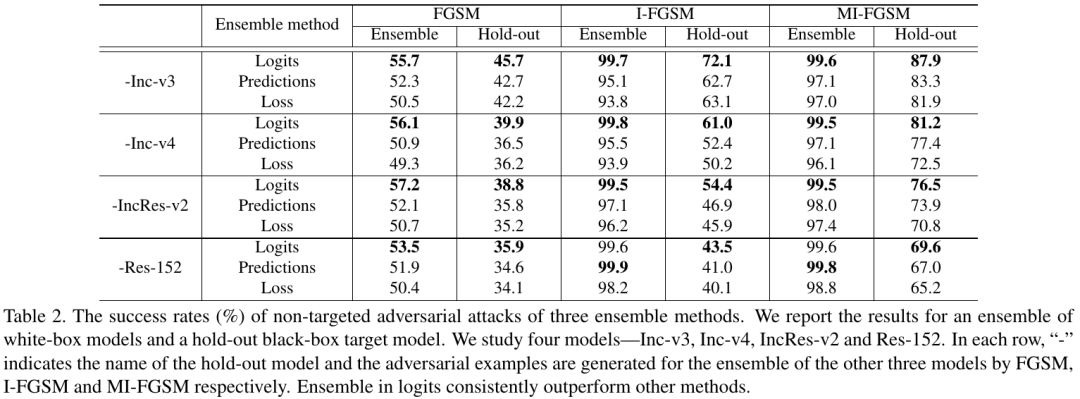
  • ensemble in logits perform better
  • MI-FGSM transfer better